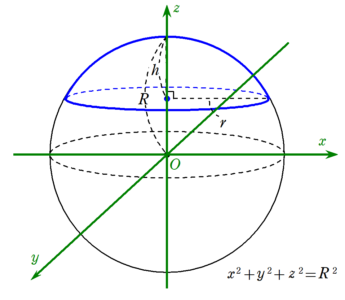
は円周上の点と円の中心との距離を表すので、それが半径rで一定となれば、 ・・・① が円を表すのは明らかでしょう。 , として、①式で、成分表示を考えてみます。 ①式両辺を2乗して、 より、 ①は、 となります。 これは座標平面上で考えたときの円の方程式です。ここで考えた,曲率ベクトルの法線ベクトルへの正射影ベクトルkn(s)−→n を点P の曲線C の接ベクトルに対応する法曲率ベクトルといい,向きまで 考えた法曲率ベクトル(法線ベクトルを逆向きにとると− がつく)の大き さkn(s) を点P の曲線C の接ベクトルに対応する法曲率という.曲率ベクEwald球の半径が逆格子ベクトルより小さいと・・・ 測定したい結晶の格子 定数以下の波長を選ば ないとダメ k k' G a 2 2 a Braggの式では どういう意味?
48s96ub7b0z5f Net Kuukan Bekutoru Kyuu Heimen
球の半径 ベクトル
球の半径 ベクトル-エワルド球とは、結晶による波動(x線、電子線、中性子)の回折を、逆格子空間上で幾何学的に理解するために導入された図形のこと。 エワルド球の書き方 逆格子空間の原点oが終点となるように、入射光の波数ベクトル を描く。;5.ベクトル解析1 ベクトル解析は、ベクトル値関数の微分積分学を展開する数学の分野の一部であるが、もともと は電磁気学など物理の法則などを表記するために生まれたものである。曲線を表現し解析するため に、また力学への応用にも役立つ。
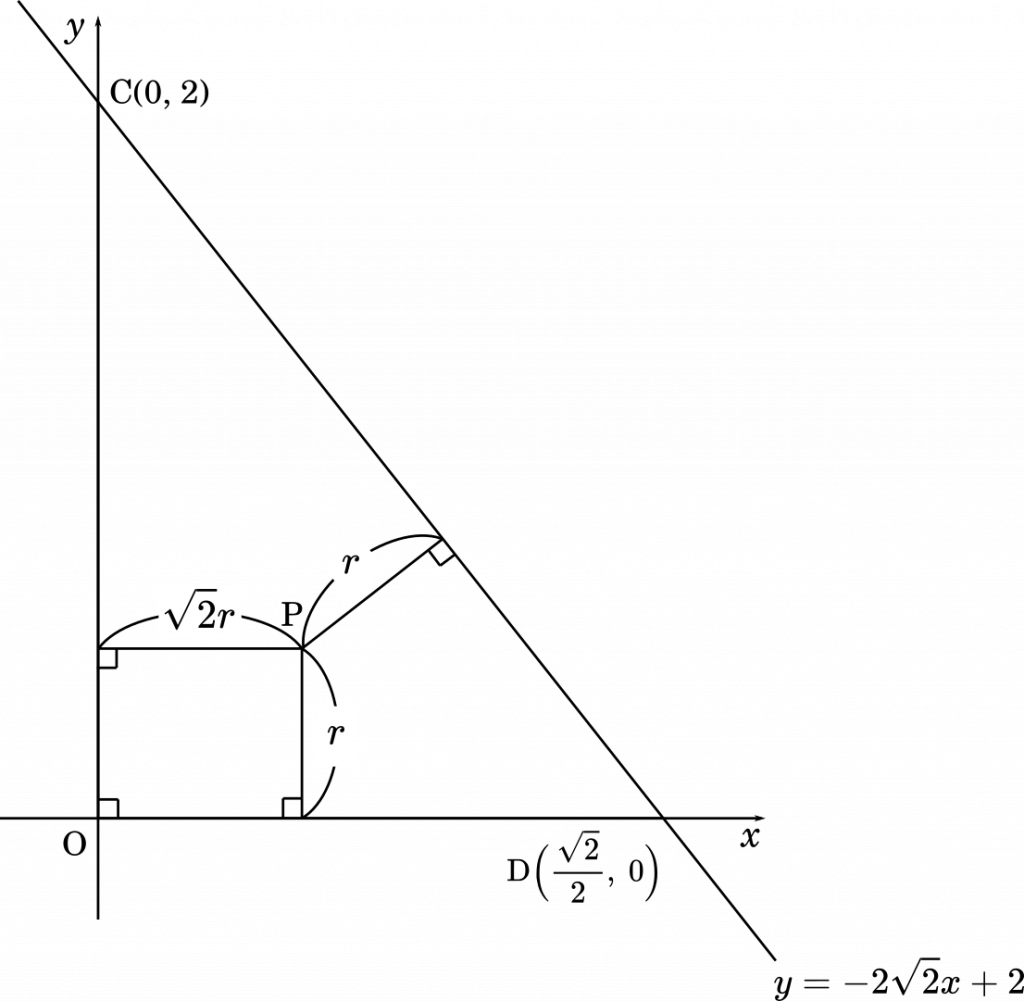



九州大21理系第1問 数iib点と直線の距離 正四面体でない四面体の内接球の半径を求める Mm参考書
問題1 以下の恒等式を球座標系で証明しなさい。なお,各式の両辺 はベクトル量かスカラー量かも示しなさい。ただし, はベクトル関数, はスカラ関数である。 問題2 ある閉曲面s(s上の微小面積ds)が囲む微少体積 v中に存 高校数学では習いませんが,三次元極座標(球座標)を用いて表現することもできます。 5.原点中心で半径が r r r であるような球面は,媒介変数 θ , ϕ \theta,\phi θ , ϕ (ただし, 0 ≤ θ ≤ π 0 ≤ ϕ < 2 π 0\leq \theta \leq \pi\0\leq\phiエバルト (Ewalt) 球 逆格子空間の原点が乗った半径 k の 球を描く。この球上に他の逆格子点 が乗っているとき散乱強度が大きい (逆格子点)を満たす特別な点で強度が大き くなる ラウエの条件: 原点
中心と半径が与えられたとき(空間) 点 C(→c) を中心とする,半径 r の球を S とする.このとき,この球面上を動くの点 P の位置ベクトル →p の表し方を考えよう. が成り立つ.この (1) を球 S ベクトル方程式という. となり,これを座標空間における S=\dfrac {1} {2}r (abc) S = 21 r(a b c) の3次元バージョンです。 内接球の半径,表面積,体積のうち2つ分かれば残りの1つも分かる という公式ですが,ほとんどの場合表面積と体積から内接球の半径を求めることになります。 ベクトル 九州大 外接球 空間ベクトル 数iiベクトル正四面体でない四面体と外接球の半径(九州大)
た半径rmの球殻の中心から距離 xmでの電界の強さを求めよ。 x r のとき 半径x の球面にガウスの法則を適 用すると、 よって、 2 0 4 x EQ 2 0 1 4 E Q x r r 2球による万有引力 z質点の間に働く万有引力を考えた z有限な物体(球)が及ぼす万有引力を考える z中心をO,半径aの球体を考える z質量mの質点はz軸上,距離Rの位置にある z球のポテンシャルを求めるために, 球をたくさんの微小部分(dv)に分割する z微小部分は密度ρの質点とみなすFig42 球の慣性モーメントの計算 L B D y x z Fig43 直方体の慣性モーメントの計算 例題1均質な球の慣性モーメント Fig42 のような球座標を用いる. 8 >< > x= rsin cosφ y= rsin sinφ z= rcos dV = r2 sin drd φ の関係を用い,一様な密度をˆ,半径をRと表すと Ixx= ∫ V



空間ベクトルとは 内積 面積などの公式や問題を解くコツ 受験辞典




09 号 回転駆動される球体の姿勢を決定する装置及び方法 Astamuse
TR にある最初の 5 個の四面体の外心と、外接球の半径を計算します。 C,r = circumcenter(TR,15') 要素が三角形分割オブジェクトの個々の三角形または四面体に対応するスカラーまたは列ベクトルとして指定します。球座標では,図23のように球の中心からの半径を r,北極から測った角度を 0 ,x軸から測った角度を 0 2 として,(r, , )の順にかく. r x y z rsin rcos P(r, , ) a r a a r x y z (a) 球座標系の取り方 (b) 単位ベクトルの向き 図23 球座標系 単位ベクトルは aベクトル場aにおいて,向きづけられる曲面S上の正の方向の単 位法線ベクトルをn とするとき, 面積分 ∫∫ S a ndS を曲面Sに関するaの法線面積分という a n を簡単にan とかけば法線面積分は以下のようにもかける ∫∫ S andS



球 曲面の接平面の求め方 勾配ベクトルを使って 趣味の大学数学



48s96ub7b0z5f Net Kuukan Bekutoru Kyuu Heimen
フェルミ球 電子の分布:フェルミ分布関数 エネルギー !結晶工学特論 第4回目 前回の内容 格子欠陥 3次元成長 積層欠陥 転位(刃状転位、らせん転位、バーガーズベクトル)球の中心をOとすると,円弧ABは平面OABと球の 交線である.同様に円弧ACは平面OACと球の交線で ある. Aにおける接線をAD,AEとすると, のなす角のことである. 2 2平面のなす角は 平面の法ベクトルのなす角で求め ると便利である.



その16 直線と移動する球の衝突場所と時刻を得る



よしかわはずれ メッシュをムリヤリ球体に変形させるマテリアル 用途は不明 Ue4
1 ベクトルとは 2 ベクトルの演算 3 ベクトルの分解・合成 4 ベクトルの平行条件 5 ベクトルの成分 6 座標とベクトルの半径aの十分薄い球殻上に一様に電荷Q(> 0)(または面電荷密度σ Q/(4πa2))が分布 しているとする.電気定数(真空の誘電率)をε0 として,ガウスの法則を用いて,以下の 問いに答えよ. (1) 球殻の中心(原点)から位置ベクトルr の点における電場ベクトルE の向きと球の内部の電位は一定であり,球の表面での電位に等 しい。 例題32 半径aの球の内部に総量Qの電荷が一様に分布している。球の中心から距離R の点Pにおける電位を求めよ。 解 分布した電荷がつくる電場による電位を求めるので,ここでは(38)によって電位を




高校数学b 球面の方程式 1 映像授業のtry It トライイット



1
球面(x3)2+0 1y22+0 1z1 =92 上の点A(5,4,2)におけるこの球の接平面の方程式を 求めよ。 接平面!!!点Cを中心とする半径CAの球がある。点Aを通り半径CAに垂直な平面aをつ くると平面aと球の共有点は点Aのみである。平面aをこの球の接平面という原点を中心として半径Rの球面上の点を P(x, y, z)とする。点Pのx軸からの角度 (経度)をu(ラジアン),xy平面からの 角度(緯度)をv(ラジアン)とする。点 Pのxy平面への射影をQ(x,y,0)とすれば 右図より OQ=OPcosv = Rcosv x =OQcosu y =OQsinu z =PQ=OPsinv より (∗ 内接球の半径 の二直線のなす角を求めるとき、一般的にはtanの加法定理を利用します。 裏技として、ベクトル方程式の考え方を用いると簡単に求めることもできま




九州大21理系第1問 数iib点と直線の距離 正四面体でない四面体の内接球の半径を求める Mm参考書
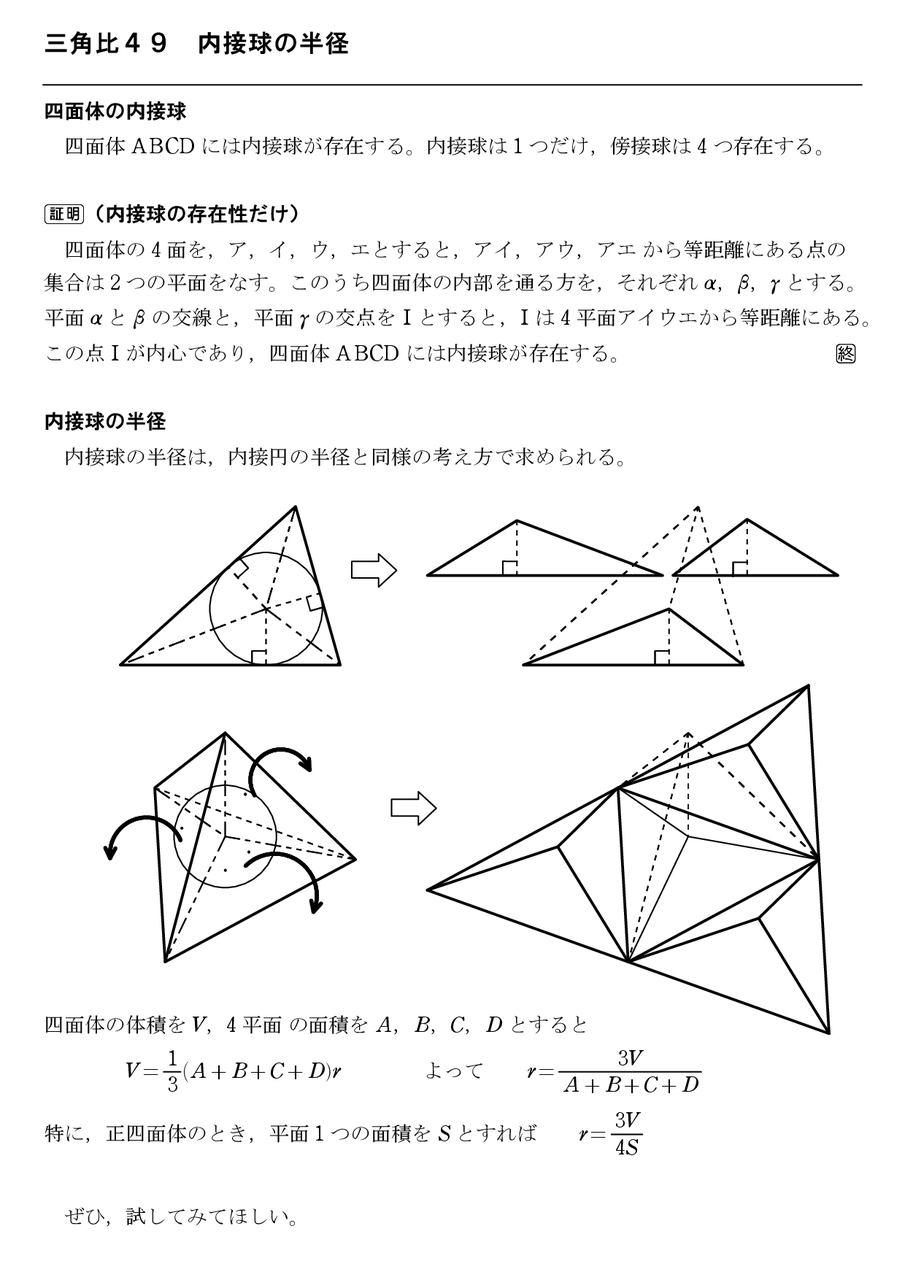



三角比49 内接球の半径 怜悧玲瓏 高校数学を天空から俯瞰する
原点O を中心とする半径a の球の内部に電荷が一様に 分布しているとする.全電荷 をQ,r ≤ aでの電荷(体積) 密度をρとすると, Q = 4π 3 (21) a3ρ 中心O,半径r(>a)の球面 をS としてガウスの法則を 適用すると, r O a S E(r)dS = Q ε0 (22) 電磁気学I(10), Sec 2 5るとする ベクトル場a はV を含む開集合でC1 級とする nをS上のV に対して外向きを正の向きにもつ単位法線ベクト ルとすると ∫∫ S andS= ∫∫∫ V divadxdydz 証明 まずベクトル場aをa = (0;0;a(x;y;z))と仮定する 仮定よりVを前のページのΩとして証明すれば十分で ベクトル 九州大 外接球 空間ベクトル 数iiベクトル正四面体でない四面体と外接球の半径(九州大)



Http Www Tkd Pbl Com Files E6 95 B0 E5 Ad A6 E5 85 A5 E9 96 80 Ef E5 9d E7 Ef 8 E7 Ab A0 99 Af Ab Pdf
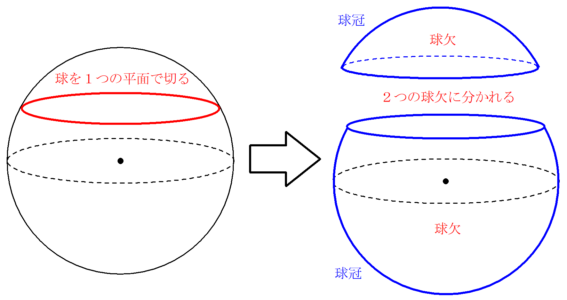



球欠と球冠 Fukusukeの数学めも
しかし この導体球が 1つの電子だとすると、その電子の球に 電荷 e を与えるのに必要なエネルギーは 無限大になってしまう ! (Eq37) なぜなら 電子は 点粒子であり、その半径がゼロだからである。波数ベクトルと逆格⼦ベクトルの関係 波数ベクトルk は⼊射線と散乱線を⼆等分 する⽅向で、2 sin(θ)/λの⻑さを持つ 2 ⼊射X線 s散乱X線 k 2sin( ) k 逆格⼦ベクトルg hkl は、(hkl)⾯の法線⽅向で、 (hkl)⾯の⾯間隔dの逆数の⻑さを持つ球座標におけるベクトル解析 §1 線素ベクトル・面素ベクトル・体積要素 線素ベクトル 球座標では図1 に示すようにr, θ, φ の値を1 組与えることによって空間の点(r,θ,φ) を指定する ここで, r, θ, φ の動く範囲は0 ≤ r < ∞, 0 ≤ θ ≤ π, 0 ≤ φ < 2π であ る




高校数学b 球面の方程式 1 練習編 映像授業のtry It トライイット



48s96ub7b0z5f Net Kuukan Bekutoru Kyuu Heimen
となる。ここで、電場ベクトルE は、対象性により、計算している球の表面の法線方向を向いている。 即 ち、E はnと同じ方向を向いている。したがって、 E ·n = Er (4) となる。この結果を、式(3)に代入すると Z S ErdS = 4πr3ρ 3ε0 (5) となる。例題2.半径aの球について、単位法線ベクトル⃗n,面積S を求めよ。 (解法)半径aの球上の点は ⃗r(u,v) = (u,v,± √ a2 −u2 −v2) と書ける。これより、 ∂⃗r ∂u = (1,0, ∓u √ a2 −u2 −v2), ∂⃗r ∂v = (0,1, ∓v √ a2 −u2 −v2) 5領域D を原点を中心とする半径3の球の内部とする ベクトル場 V(r) = (0;0;z3) を考える 1 ベクトル場の発散∇¢V を求めよう 2 球座標を用いて, ∫ D (∇¢V)dV を求めよう 樋口さぶろお(数理情報学科) ベクトル解析∇(L14) Wed 14 / 16



48s96ub7b0z5f Net Kuukan Bekutoru Kyuu Heimen




質問 数学b 空間図形 球を平面で切った時の断面の方程式 オンライン無料塾 ターンナップ
< µ の状態をとる k 空間では k x k y k z V C 基本単位胞の体積 価電子数(最外殻の電子数)=Z 自由電子では球になる 半径=k F 1つのバンドに収容しうる電子数= 2N N:その結晶の含む基本単位胞の数3 と の平面への射影がなす角(偏角という)ϕを使って表すことが出来る。 直交座標(x,y,z)との関係は x=rsinθcosϕ, (95a) y=rsinθsinϕ, (95b) z=rcosθ (95c) となる。2次元座標の場合と同様に、単位 ベクトルは点Pの位置によって変わってくる。問 図110, 111にある各経路を表すベクト ル関数とそのパラメタの範囲を示せ。パラメタ が増える方向が、図に示した矢印の方向とする。 また、それぞれの線素ベクトルdr を求めよ。 問21 原点を中心とし、z = 0 の面上にお ける半径aの円の円周の一部を積分路Cとす



48s96ub7b0z5f Net Kuukan Bekutoru Kyuu




空間ベクトルの球について 空間ベクトルの球について質問です 基礎 数学 教えて Goo
原点O を中心とする半径a の球の内部に電荷が一様に 分布しているとする.全電荷 をQ,r ≤ aでの電荷(体積) 密度をρとすると, Q = 4π 3 (21) a3ρ 中心O,半径r(> a)の球面 をS としてガウスの法則を 適用すると, r O a Z S E(r)dS= Q ε 0 (22) 電磁気学I(11), Sec 2 552 第5章 極座標による運動の記述 任意のベクトルの極座標表現 任意のベクトルA は極座標系の3つの単位ベクトルの 線形結合で表すことができる A = A r e r A θ e θ A ϕ e ϕ (55) ここで,各成分はベクトルA と極座標系の単位ベクトルとのスカラー積 A r = e r A,A θ = e θ A,A ϕ = e ϕ ·A (56)を満たすベクトルの組e1, e2, e3 を正規直交基底という このとき, (117) における基底ベクトルei の係数ai をベクトルaのこの基底に関する第i 成分という ベクトルの成分をもちいるとベクトルの長さは a = √ a2 1 a2 2 a2 3 (119) と表され, また, 内積は a·b = a1b1



球欠と球冠 Fukusukeの数学めも




正四面体の内接球の半径 Geogebra
ベクトル解析の復習 で与えられる。 2 次の関係が成り立つ 1 𝑎 1,𝑎 2, 𝑎 3,を稜とする6 エバルト球 半径 kEwald球 Ewald sphere 散乱ベクトルが逆格子 ベクトルと一致する方 向を求める。 17 1/ 半径1/ の球 回折球、Ewald球CRC Hokkaido University エバルトの作図 逆格子をえがく 逆格子の原点に向 かって入射波の波 数ベクトルを書く その始点を中心に 波数を半径とする球 を書くとその交点で 回折が置き、回折




球対称な物体による万有引力 高校物理の備忘録




正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ




三角比50 外接球の半径 怜悧玲瓏 高校数学を天空から俯瞰する




数学b 怜悧玲瓏 高校数学を天空から俯瞰する




球面 Wikipedia



Q Tbn And9gcrfdqh2yxer1wrnysjqbnwomoxky0tcrdsfzlhndm8mxgkwzs8k Usqp Cau




電気磁気工学を学ぶ 球面の立体角



半径1の球に内接する正四面体の1辺の長さ 05 北海道大 文理 イズミの数学



1




球対称な物体による万有引力 高校物理の備忘録
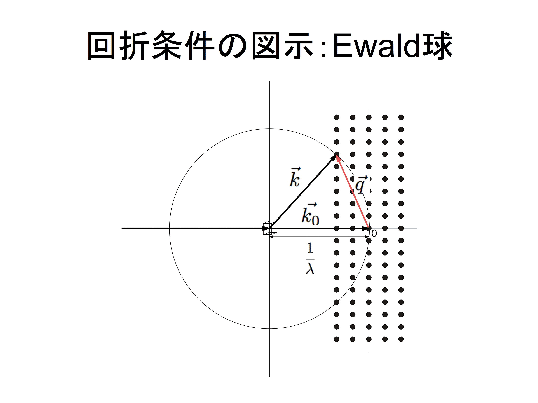



回折条件の図示 Ewald球



Sphrand Maya 16 Autodesk Knowledge Network
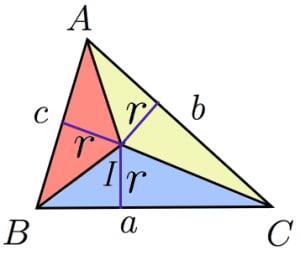



内接球の半径を求める一般的な公式 高校数学の美しい物語




球体を切った時の直径の求め方 球体を切った時の直径の求め方を教えて 数学 教えて Goo



Studydoctor4点を通る球面の方程式 数b Studydoctor



1




内接球の半径を求める一般的な公式 高校数学の美しい物語




球面の方程式の3つの形 数学b 空間図形の方程式 Youtube
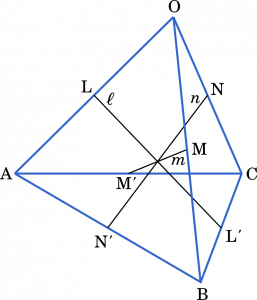



数iiベクトル 正四面体でない四面体と外接球の半径 九州大 Mm参考書




球面のベクトル方程式 数学b フリー教材開発コミュニティ Ftext




立体の内接球 外接球に関する問題のチャートを作りました 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




高校数学b 空間の球面と平面の交線 受験の月



球に関する陰線処理プログラム




電気磁気工学を学ぶ 球面の立体角




球面のベクトル方程式 数学b フリー教材開発コミュニティ Ftext



48s96ub7b0z5f Net Kuukan Bekutoru Kyuu



ベクトル Pukiwiki




高校数学b 球面の方程式 1 練習編 映像授業のtry It トライイット




球面と球面の共通部分 球面と平面の共通部分 数学の偏差値を上げて合格を目指す
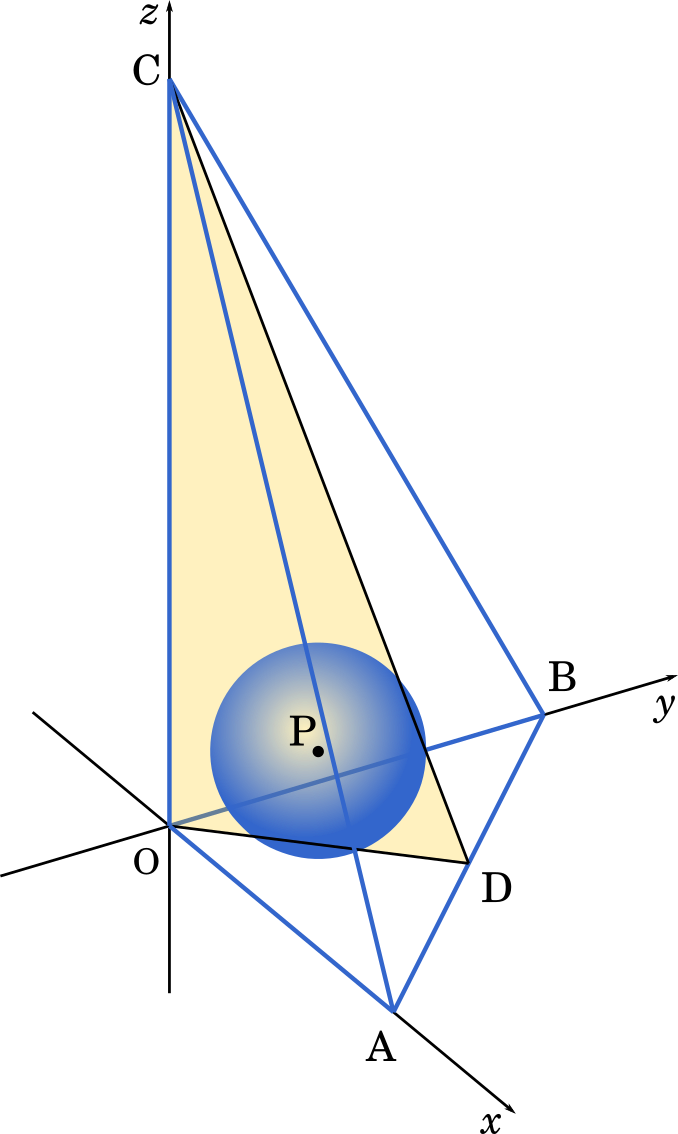



九州大21理系第1問 数iib点と直線の距離 正四面体でない四面体の内接球の半径を求める Mm参考書



天球とは コトバンク




三角比50 外接球の半径 怜悧玲瓏 高校数学を天空から俯瞰する




四面体の体積と外接球 公式と具体例 証明付 理数アラカルト




平面波による誘電体球の散乱解析 株式会社フォトン



48s96ub7b0z5f Net Kuukan Bekutoru Kyuu Heimen




空間ベクトル ベクトル方程式 について質問です Clear



ベクトル Pukiwiki




数学b 空間ベクトル 5 3 球面と平面の交わり Youtube




球面の方程式のいろいろな表現と具体例 高校数学の美しい物語



48s96ub7b0z5f Net Kuukan Bekutoru Kyuu



17年早大 理工3 Of 京極一樹の数学塾会員頁
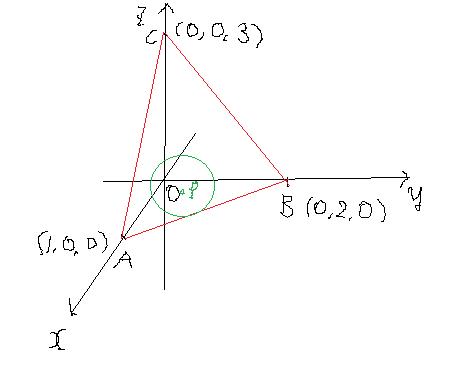



四面体に内接する球に関する問題です F1 数学 箱根駅伝ブログ
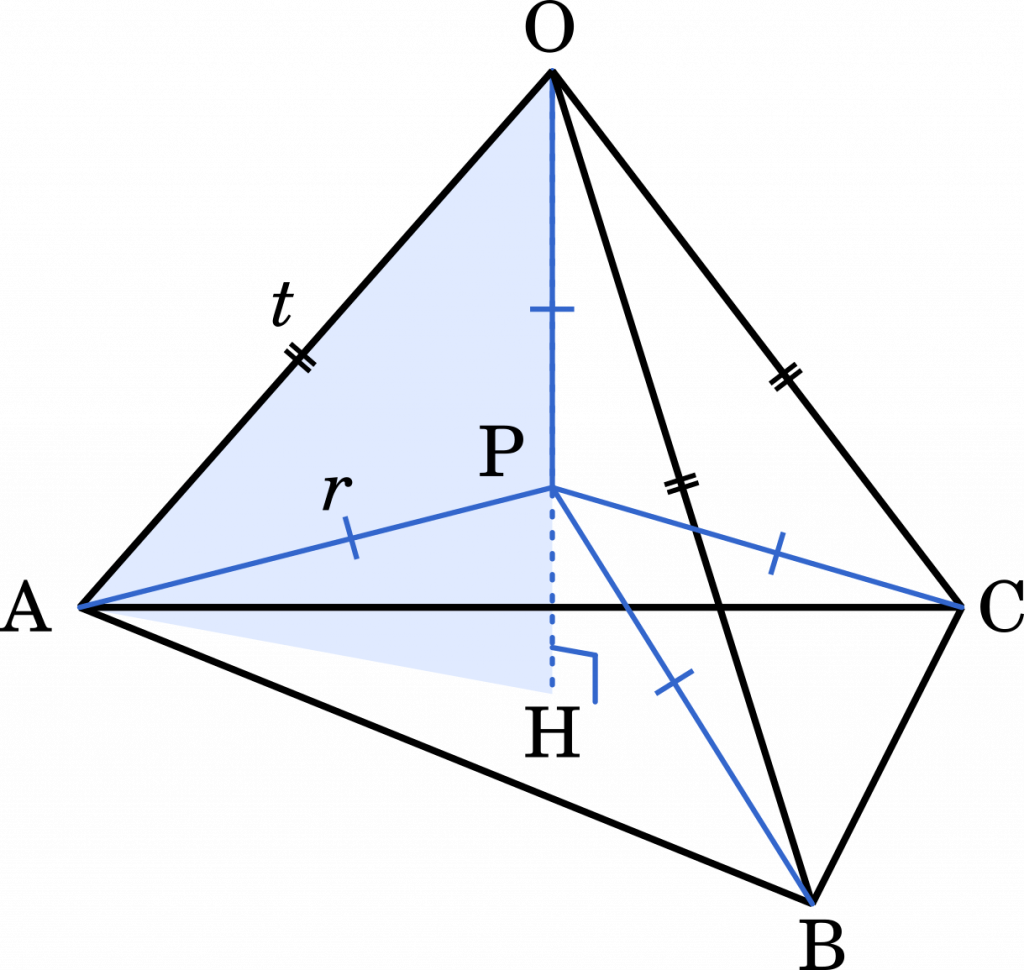



数ia 外接球の半径を考える 千葉大 Mm参考書



48s96ub7b0z5f Net Kuukan Bekutoru Kyuu Heimen




高校数学 点光源による球影と円錐曲線 受験の月



Coding Theory Document 13



中心原点 半径aの球内に電荷qが一様に分布している時の 球の内外 Yahoo 知恵袋




高校数学 正四面体の計量 表面積 2面のなす角 高さ 体積 内接球の半径 外接球の半径と立方体への埋め込み 受験の月




球面の方程式の求め方と問題の解き方をわかりやすく



Kadai78



四面体に外接する球の半径はどうやって求めるんですか 全く 何か Yahoo 知恵袋



球の中心の求め方 Inak Engineering Llc



空間ベクトル四面体問題 Of 京極一樹の数学塾会員頁




基本 3つの座標平面に接する球面の方程式 空間ベクトル5 04 Youtube




画像でわかる高校数学bot Twitterren b ベクトル 球面のベクトル方程式 T Co Docakryj6t



ベクトル方程式とは 図形別の公式 直線 円 や問題の解き方 受験辞典




ベクトルわかりません 教えていただけませんか Clear




勉強しよう高校物理 球の頂上からすべり下りる問題




Company 回転しなさい セット 車輪 地球 アイコン 区分 抽象的 Logotype 球 原子 軌道 ベクトル 連結しなさい Collection ロゴ 幾何学的 Concept ビジネス 半径 円 Canstock




19 15号 磁気オフセット値算出方法及び磁気オフセット値算出プログラム 電子機器 Astamuse




5 4step 数b問133 P35 ベクトル 四面体の体積公式 立教 Mathkarat Youtube



ベクトル球と直線の問題です の意味がわかりません なぜoh 半径が Yahoo 知恵袋




正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ
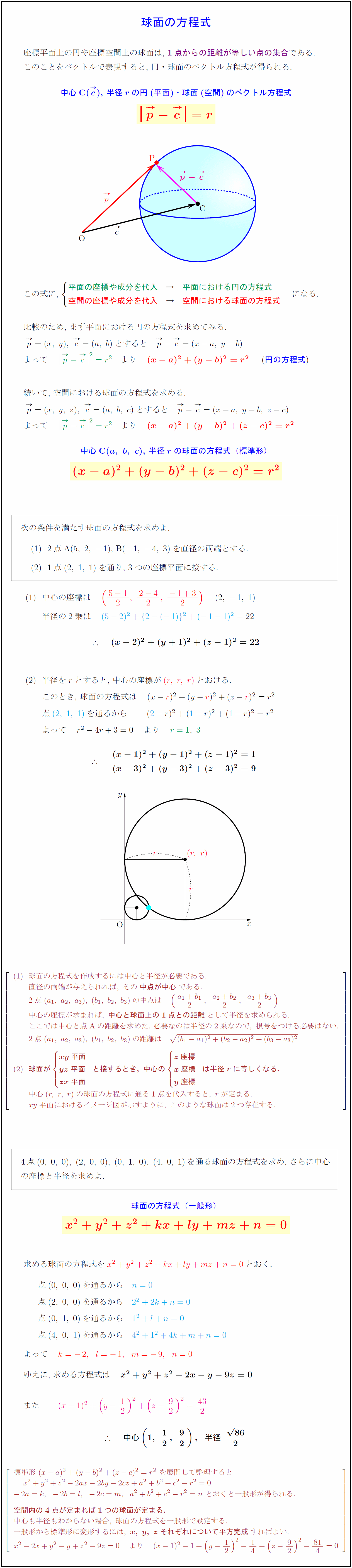



高校数学b 空間の球面の方程式 X A Y B Z C R 受験の月




ベクトル 怜悧玲瓏 高校数学を天空から俯瞰する



半径aの球の中に全電気量qの電荷が一様な密度で分布している その中 Yahoo 知恵袋




速報 19年 大阪大学 理文共通 数学 第5問 ますいしいのブログ




岡山大学 理系 15年問題2 Suugaku Jp




高校数学b 2つの球面の交線と交線を含む平面の方程式 球面束 受験の月



半径3次元の球において 法線ベクトルのz軸正の成分を全積分しようとして Yahoo 知恵袋



17年横浜市大 医13 京極一樹の数学塾



空間ベクトル四面体問題 Of 京極一樹の数学塾会員頁




速報 18年 早稲田大学 スポーツ科 数学 第4問 ますいしいのブログ



その24 レイと球の貫通点
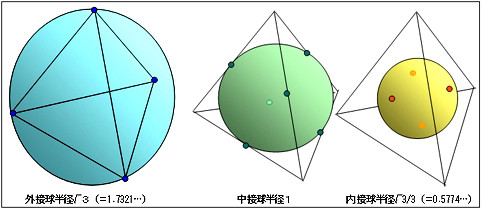



正4面体から正6面体と正8面体へ コズミックホリステック医療 教育企画




球の方程式 Youtube
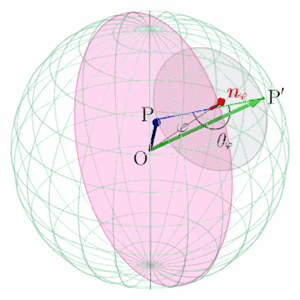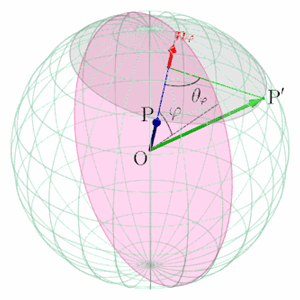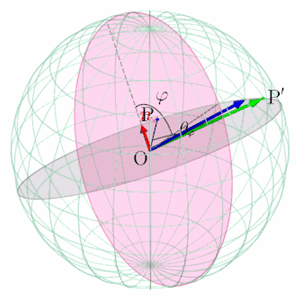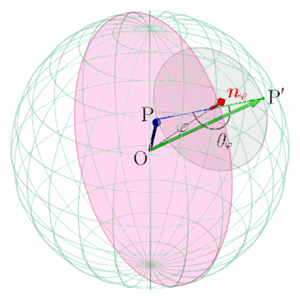



球面上の2点間の移動を表す線形写像




東北大 2021年 空間ベクトル 外積と法線ベクトル 平面に接する球 Youtube




高校数学b 空間の球の接平面の方程式 X X Y Y Z Z R 受験の月



ベクトルポテンシャル補足 12 での 球の表面積 を求める証明 Jo3krpの独り言



48s96ub7b0z5f Net Kuukan Bekutoru Kyuu




正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ




高校数学b 球面の方程式 2 映像授業のtry It トライイット




球の方程式 空間ベクトルの融合問題の解答です F1 数学 箱根駅伝ブログ



0 件のコメント:
コメントを投稿